画像 y=x^3 reflected about the x axis 146993-Y x 3 reflected about the x-axis
Reflect Over XAxis Formula The following formula is used to reflect a coordinate point about the xaxis (X2,Y2) = (X1,Y1) * (1,1) Where X2 and Y2 are the new reflected coordinates;If f(x) = x 3 is changed to f(x) = (x 3) 3 2, how is the graph transformed?The correct answer isTranslated according to the rule (x, y) →(x 2, y 8) and reflected across the yaxisExplanationA translation using the rule (x, y) →(x 2, y 8) adds 2 to the xcoordinate and 8 to the ycoordinate

Reflecting A Shape In The X Axis Using Cartesian Coordinates Key Stage 3
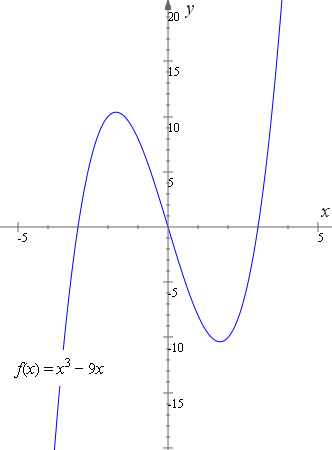
Y x 3 reflected about the x-axis
Y x 3 reflected about the x-axis- 🔴 Answer 3 🔴 on a question What set of reflections would carry hexagon ABCDEF onto itself?Reflecting functions examples CCSSMath HSFBF Transcript We can reflect the graph of any function f about the xaxis by graphing y=f (x) and we can reflect it about the yaxis by graphing y=f (x) We can even reflect it about both axes by graphing y=f (x) See how this is applied to solve various problems
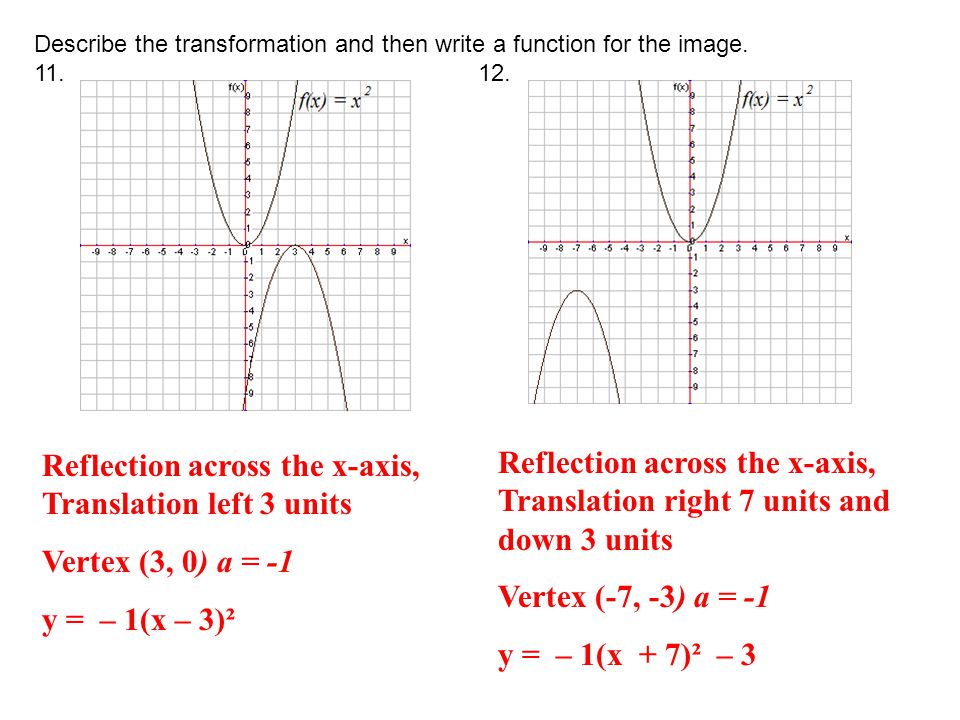



8 3 Notes Handout Ppt Video Online Download
In this video, you will learn how to do a reflection over the line y = x The line y=x, when graphed on a graphing calculator, would appear as a straight line cutting through the origin with a slope of 1 For triangle ABC with coordinate points A (3,3), B (2,1), and C (6,2), apply a reflection over the line y=x Find the slopeintercept form of the line passing through the point (8,7) and parallel to the line y = – 2x – Point c is (1, 3) What is point c reflected over the xaxis, the yaxis and origin/both axes What is the distance;A reflection across xaxis is nothing but folding or flipping an object over the x axis The original object is called the preimage, and the reflection is called the image If the preimage is labeled as ABC, then t he image is labeled using a prime symbol, such as A'B'C' An object and its reflection have the same shape and size, but the figures face in opposite directions
The problem of Y=X^2 is reflected across the X axis scale vertically by a factor of 4/3 What is the equation for the new problem Answers 1 Get Other questions on the subject Mathematics Mathematics, 1600, Sallyjoe9630 How much of 10% hci and 35% hci would be needed to mix and produce 60liters of 25% hciThe graph of f (x) = x is reflected over the yaxis and horizontally stretched by a factor of 3 8 (x) = a The graph of f (x) = r is vertically compressed by a factor of then shifted to the left 9 units and up 4 units 3 8 (x) = b The graph of f (x) = x2 is horizontally stretched by a factor of 6, then shifted to the left 2 units and down 9 Correct answer Reflect (3, 4) across the yaxis Then reflect the result across the xaxis
What you'll find in this video1) What are reflections?In a reflection transformation, all the points of an object are reflected or flipped on a line called the axis of reflection or line of reflection Example A reflection is defined by the axis of symmetry or mirror lineIn the above diagram, the mirror line is x = 3Functions of graphs can be transformed to show shifts and reflections Graphic designers and 3D modellers use transformations of graphs to design objects and images




Reflection Of Points In The X Axis Worksheet
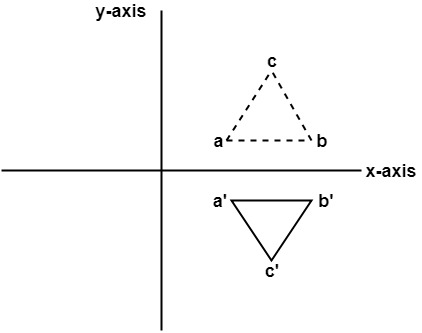



Computer Graphics Reflection Javatpoint
Categories Mathematics Leave a Reply Cancel reply Your email address will not be published CommentReflected over the xaxis and shifted down 3 Describe the transformations y = x 3 stretched by a factor of 4 and shifted up 1Math Precalculus Precalculus questions and answers Suppose the graph of y = 9x2 3x 3 is reflected across the yaxis The equation of the new graph will be y (You do not need to simplify) Question Suppose the graph of y = 9x2 3x 3 is reflected across the yaxis The equation of the new graph will be y (You do not need to simplify)
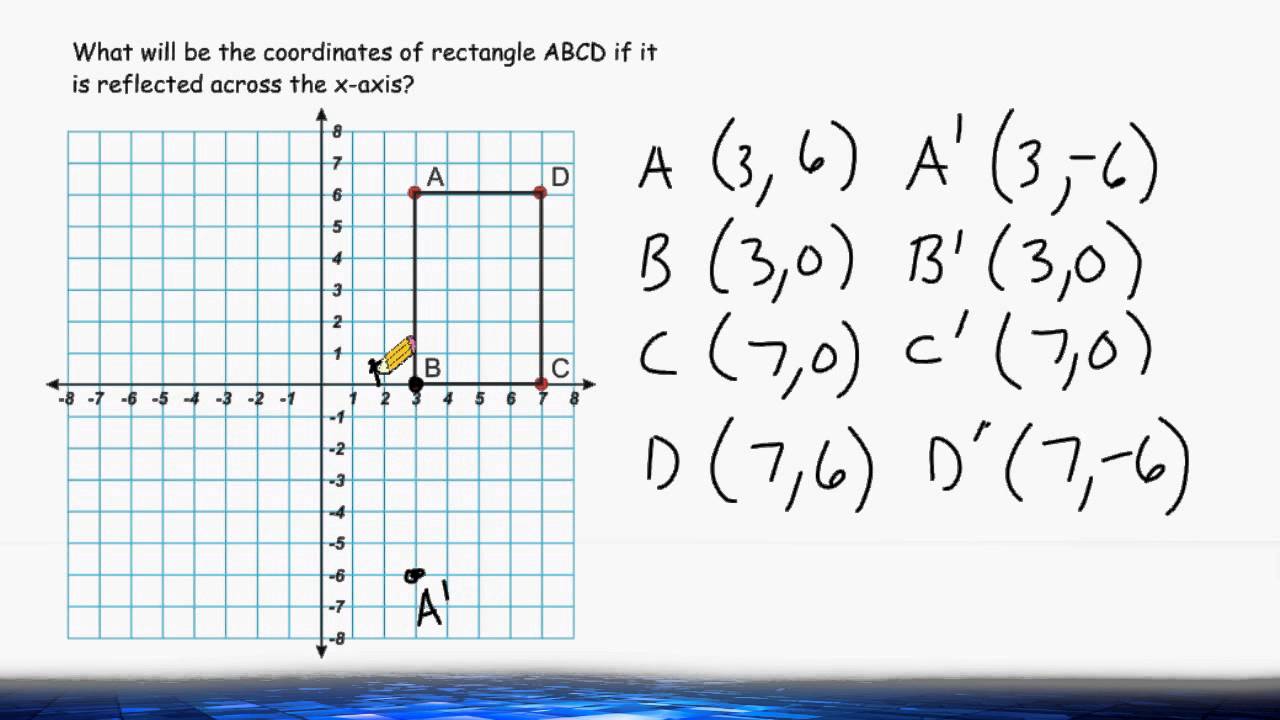



Transformations Reflection Across The X Axis Youtube
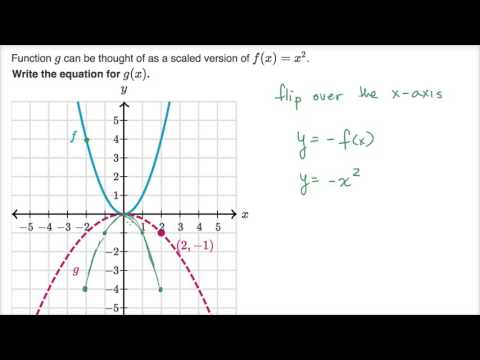



Scaling Reflecting Parabolas Video Khan Academy
Replace x with (x) an dyou get y = 2 * x 3 which becomes y = 2x 3 that's your reflected equation the graph of both equations will show you that the equations are symmetric about the yaxis this means that x = 3 becomes y = 2x 3 which becomes y = 9 in the original equation this means that x = 3 becomes y = 2x 3 which becomes y = 9 in the reflected equation the For example, when point P with coordinates (5,4) is reflecting across the Y axis and mapped onto point P', the coordinates of P' are (5,4)Notice that the ycoordinate for both points did not change, but the value of the xcoordinate changed from 5 to 5 You can think of reflections as a flip over a designated line of reflectionAnswer choices 3 units right, 2 units up, reflected across the yaxis



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics



Cw 18 Reflections
Question reflecting point in the x axis ,yaxis what will be the coordinates of the image if point A (2;3) reflect in the x axis Answer by Cromlix(4381) (Show Source)A reflect across the xaxis, translate 3 units to the left, translate down 2 units b reflect across the xaxis, translate 3 units to the right, translate up 2 units c translate 3 units to the left, translate down 2 units d translate 3 units to the right, translate up 2 unitsIf the graph of y=x is compressed vertically by a factor of 1/3, reflected about the xaxis and translated 3 unit(s) left and 5 unit(s) up, what is the equation of the new graph?




Solved A F X X G X X 3 O Reflect About The Chegg Com



Reflect Triangle Over X Axis Y Axis Y X Y X Geogebra
12 If the figure is a regular polygon, Find the value of x (6x – 21)° Categories Biology;The light path would be alone The line y equals two X minus four So I would have a wider septic negative for with a scope of to So the light path would be through the focus on the right side heads that would reflect back to the focus on the left side What should be two units So they're left of the sector It should be at the point Correct answer to the question Reflect (8, 3) in (a) the xaxis and (b) the yaxis



Determine Whether A Function Is Even Odd Or Neither From Its Graph College Algebra



Ex Reflect A Point About The X Axis Y Axis And The Origin Math Help From Arithmetic Through Calculus And Beyond
Reflection over the xaxis A reflection over the xaxis can be seen in the picture below in which point A is reflected to its image A' The general rule for a reflection over the xaxis $ (A,B) \rightarrow (A, B) $ If we reflect (4,3) across y axis, the point becomes (4,3) if you visualise it When we reflect this in the 'x' axis, we get (4,3), if you visualise it This is a lot faster than the matrix method and much more simple Reflection across yaxis matrix is Reflection across xaxis is now we multiply the pointsGraph functions using reflections about the xaxis and the yaxis Another transformation that can be applied to a function is a reflection over the x – or y axis A vertical reflection reflects a graph vertically across the x axis, while a horizontal reflection reflects a graph horizontally across the y axis
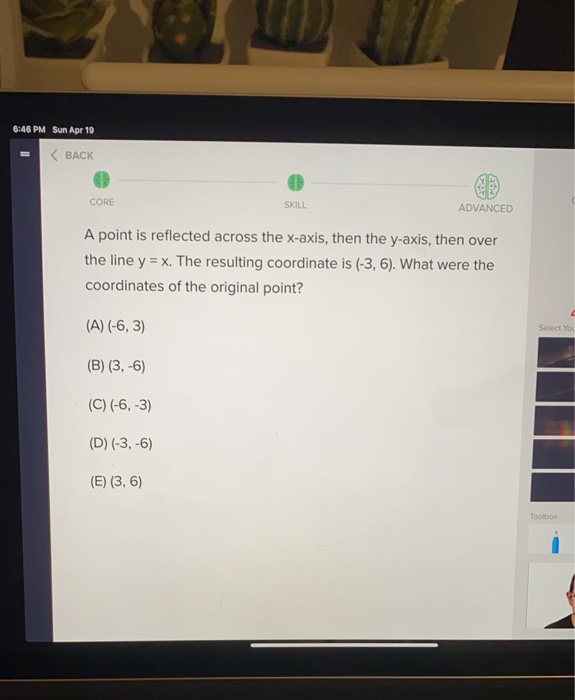



Solved 6 46 Pm Sun Apr 19 Back Core Skill Advanced A Point Chegg Com
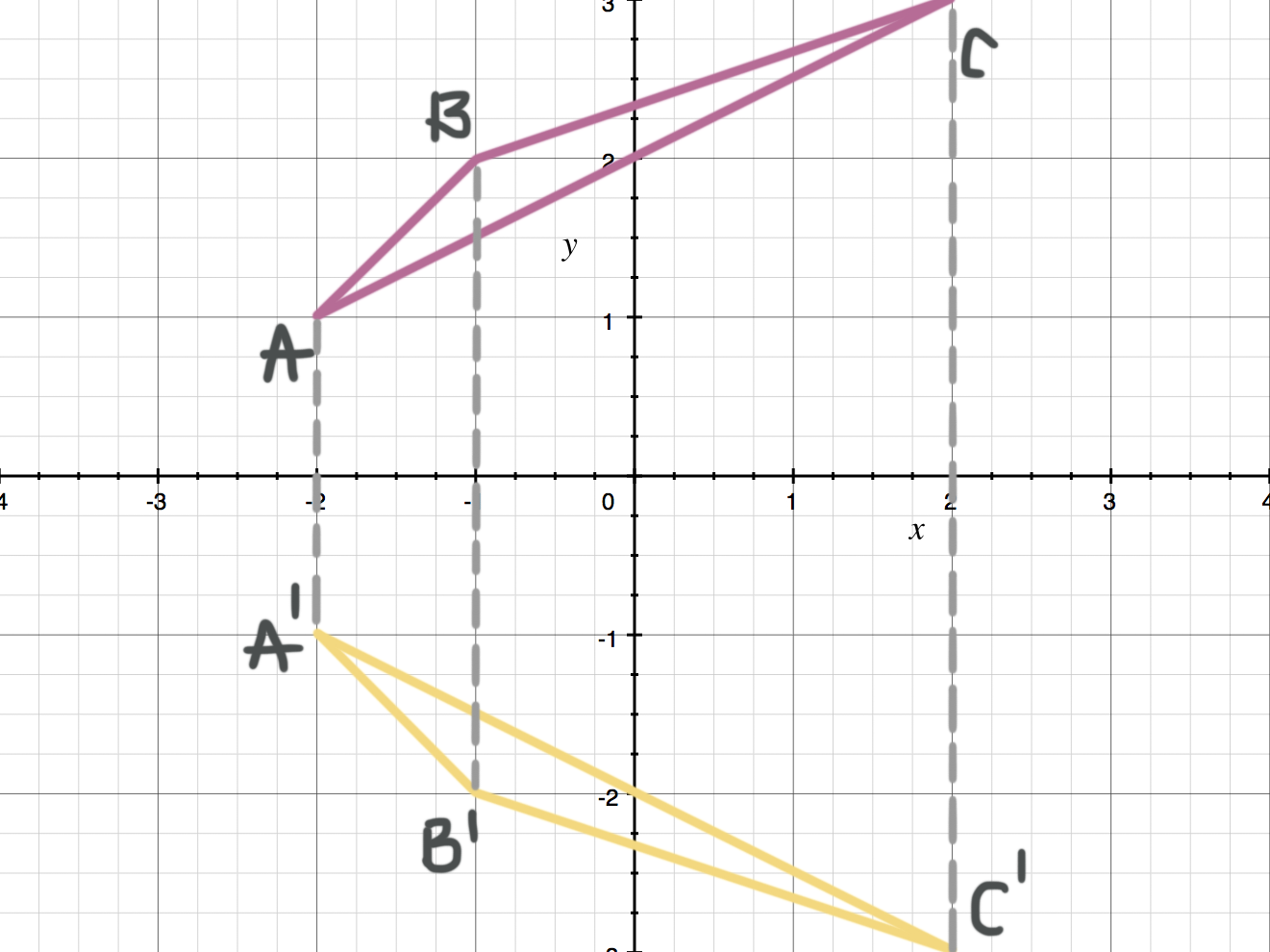



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
You want to reflect (7,3) in yaxis Let this point be P(7,3) and let the point to find be Q(x,y) Now when the point is reflected in y axis, the ycoordinate of the point remains same The sign of xcoordinate changes The point P is in the third quadrant so it's reflection in yaxis will be in the fourth quadrant👉 Learn how to reflect points and a figure over a line of symmetry Sometimes the line of symmetry will be a random line or it can be represented by the xRelated Pages Properties Of Reflection Transformation More Lessons On Geometry What is Reflection?
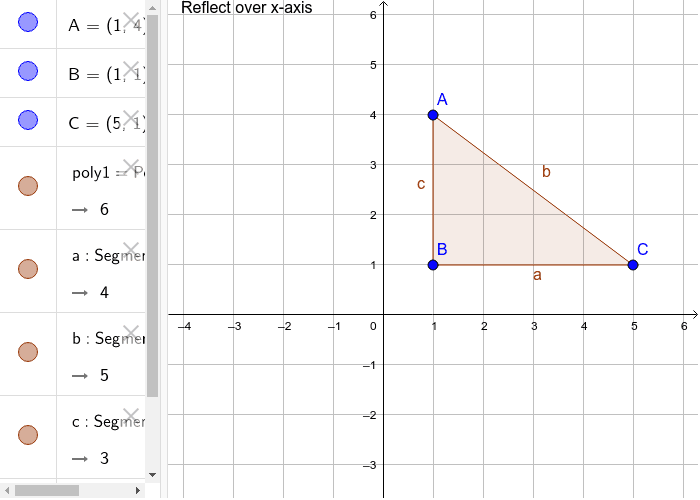



Reflect Over X Axis Y Axis Y X And Y X Geogebra
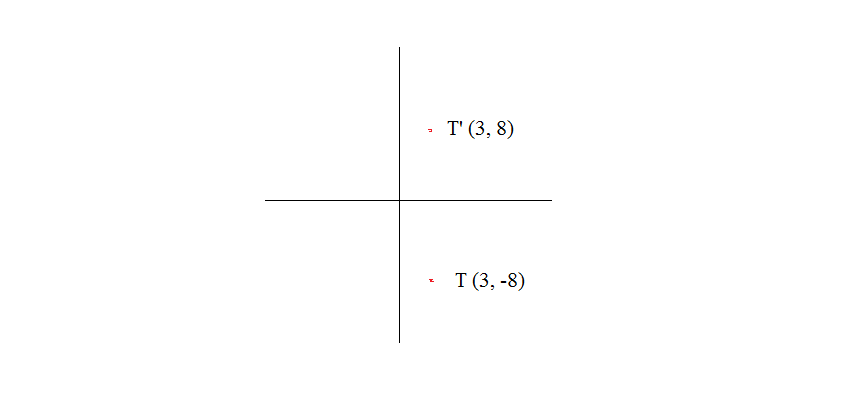



Point T 3 8 Is Reflected Across The X Axis Which Statements About T Are True Socratic
you graph at the (3) point on the y axis it should look like a vertical line across the y axis on where it says 3 A triangle has points A(2, 3), B(2, 6), and C(7, 3) and is reflected over the xaxisIn addition to shifting, compressing, and stretching a graph, we can also reflect it about the xaxis or the yaxis When we multiply the parent function latexf\left(x\right)={b}^{x}/latex by –1, we get a reflection about the xaxis When we multiply the input by –1, we get a reflection about the yaxis For example, if we begin by graphing the parent function latexf\left(x\right)={2}^{x}/latex, we can then graph the two reflectionsY= (2(x3))⁶3 3 ,that is outside, means translated 3 units up, 3 ,that in the parenthesis, (x3) means shifted 3 units to the left (2) means compressed horizontally " " in front means reflected over the xaxis The graph is compressed horizontally by a factor of 2, shifted left 3, reflected over the xaxis, and translated up 3




Section 4 3 Reflecting Graphs Symmetry Objective To Reflect Graphs And To Use Symmetry To Sketch Graphs Ppt Download




Reflection Over The Line Y X Math Showme
Every point below the xaxis is reflected to its corresponding position above the xaxis Contents Reflection over the xaxis for Sets of Coordinates (x, y),Construct a line from A parallel to the xaxis, determine the distance from A to the xaxis along this parallel line, find a new point on the other side of the xaxis that is equidistant from the xaxis(018)2) Reflection over xaxis(036)3) Rigid Motion (214)4) Reflection over yaxis (1)5) Reflect




Reflection Rules How To W 25 Step By Step Examples



1
Correct answers 3 question What steps transform the graph of y=x^2 to y= (x 3)^2 2?A shape can be reflected in the xaxis If point on a shape is reflected in the xaxis, the xcoordinate stays the same, but the ycoordinate changes sign (becomes negative if it is positive and vice versa) The image below shows a point on a shape being reflected in the xaxis The point A has Cartesian coordinates (3, 1)The concept behind the reflections about the xaxis is basically the same as the reflections about the yaxis The only difference is that, rather than the yaxis, the points are reflected from above the xaxis to below the xaxis, and vice versa




8 3 Notes Handout Ppt Video Online Download




The Graph Of Y X Is Reflected Across The X Axis And Then Scaled Vertically By A Factor Of 7 What Brainly Com
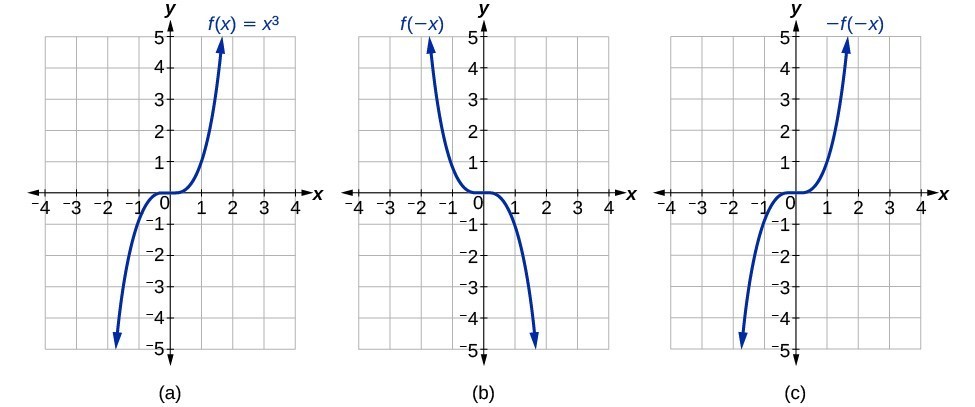
Y = x3 y = x 3 The parent function is the simplest form of the type of function given y = x3 y = x 3 For a better explanation, assume that y = x3 y = x 3 is f (x) = x3 f ( x) = x 3 and y = x3 y = x 3 is g(x) = x3 g ( x) = x 3 f (x) = x3 f ( x) = x 3 g(x) = x3 g ( x) = x 3 Note that when a function y=f(x) is reflected about the xaxis, the new equation is y=f(x) This means that when reflected about the xaxis, all original values of y are multiplied byThe graph of y=x^2 is reflected in the xaxis and translated 3 units right and 2 units up Write an equation for the function in vertex form and in standard form




Transformations Reflection Across The X Axis Youtube




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation
Which statement accurately describes how to reflect point A (3, ?1) over the yaxis?The transformation from the first equation to the second one can be found by finding a a, h h, and k k for each equation y = a√x− hk y = a x h k Factor a 1 1 out of the absolute value to make the coefficient of x x equal to 1 1 y = √x y = x Find a a, h h, and k k for y = √x y = x a = 1 a = 11 Answer (i) The reflection in xaxis is given by Mx (x, y) = (x, y) A' = reflection of A (3, 2) in the x axis = (3, 2) The reflection in origin is given by MO (x, y) = (x, y) (ii) The reflection in yaxis is given by My (x, y) = (x, y) The reflection of A (3, 2) in yaxis is (3, 2)
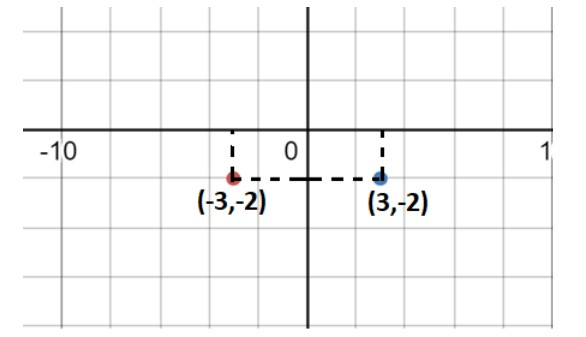



Find The Reflection Of The Point 3 2 In Yaxis Class 9 Maths Cbse
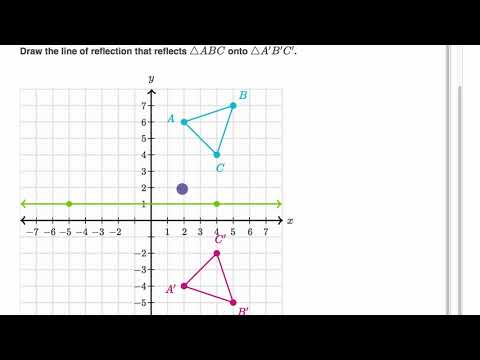



Determining Reflections Video Khan Academy
3 С D 2 В A F 3 4 5 Oy = x, Xaxis, y = x, yaxis xaxis, y = xThe xcoordinate becomes the ycoordinate and the ycoordinate becomes the xcoordinate The image below shows a point on a shape being reflected in the line y = −x The point A has Cartesian coordinates (−3, 5) The reflected point A' has Cartesian coordinates (−5, 3) The xcoordinate of A (−3) has its sign changed (3) and becomes theReflect Over XAxis Definition
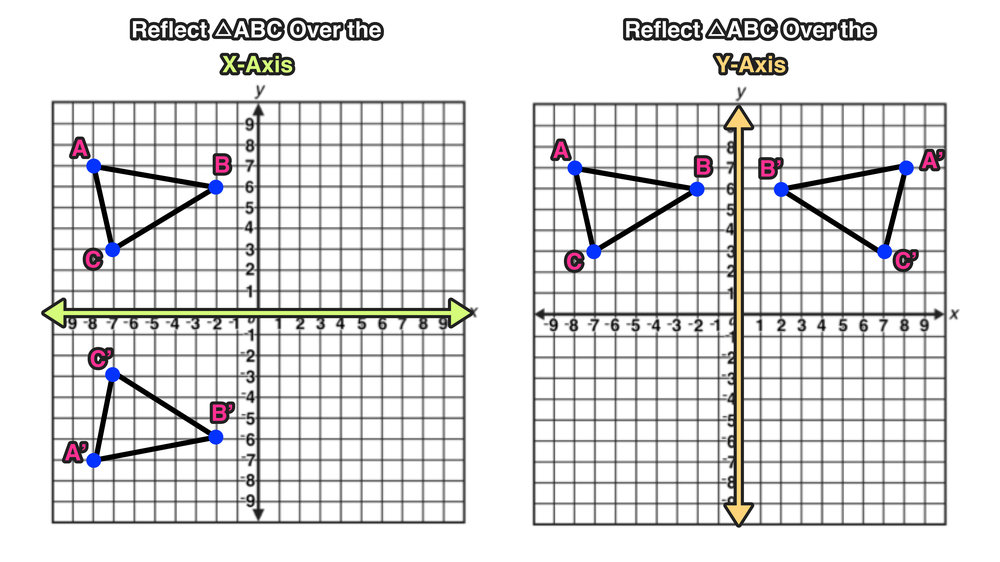



Reflection Over The X And Y Axis The Complete Guide Mashup Math
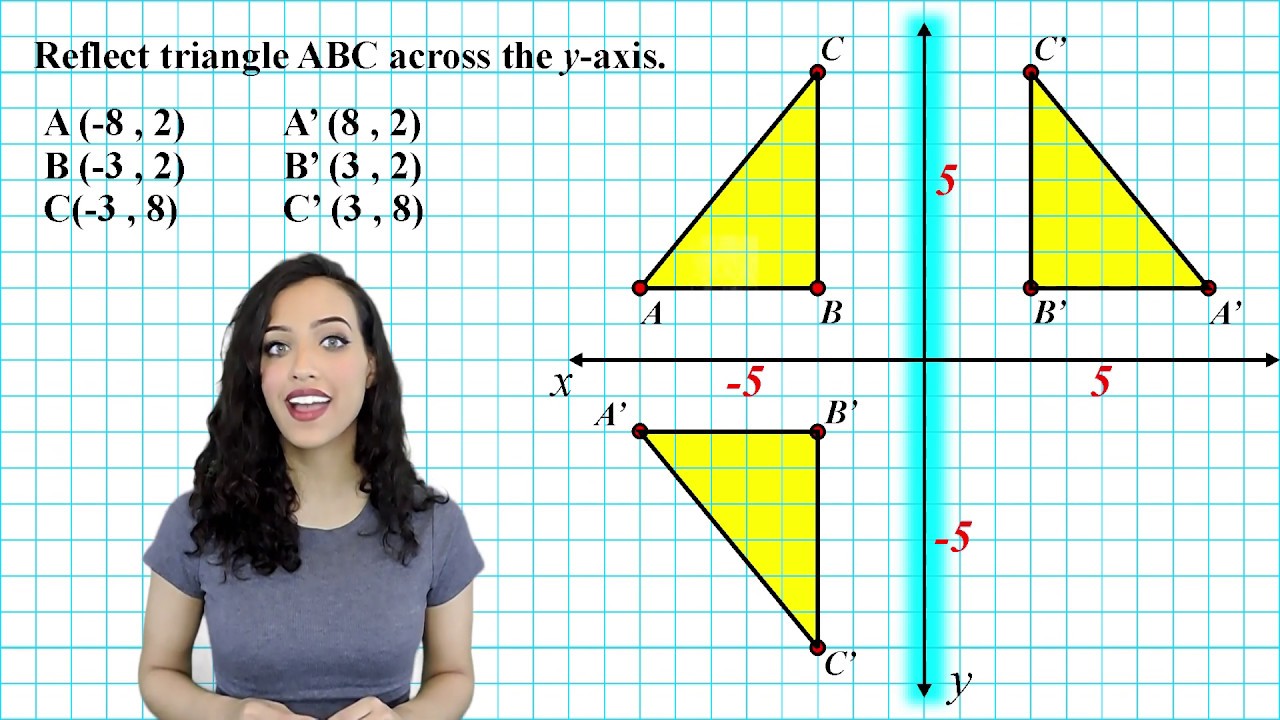



Reflection Across The X And Y Axis Youtube
Since we do reflection transformation through the yaxis, we have to replace "x" by "x" in the given function y = √x Step 2 So, the formula that gives the requested transformation is y = √x Step 3 The graph y = √x can be obtained by reflecting the graph of y = √x through the yaxis using the rule given below1 answer The given parabola y = ax2 bx c y = a x 2 b x c doesn't intersect the Xaxis and passes from the points A(−2,1) A ( − 2, 1) and B(2,9) B ( 2, 9) Find all the possible values of the x coordinates of the vertex of this parabolaX1 and Y1 are the original coordinate points;
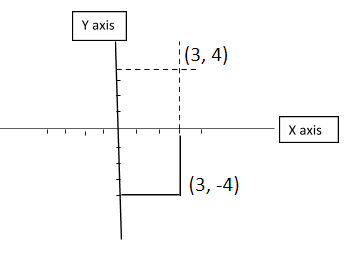



Write The Reflection Of Point B 3 4 In Xaxis And Y Class 11 Maths Cbse
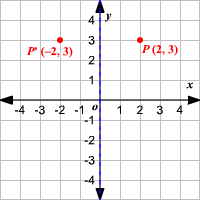



Reflections
Q Reflect over xaxis Which point would be at (3, 6) Q If the dotted figure is the image, the original figure was reflected over the Q State the line of reflection Q Reflection over the xaxis is a type of linear transformation that flips a shape or graph over the xaxis Every point above the xaxis is reflected to its corresponding position below the xaxis;
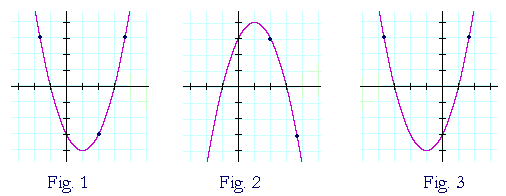



Reflections Of A Graph Topics In Precalculus




Reflecting A Shape In The X Axis Using Cartesian Coordinates Key Stage 3
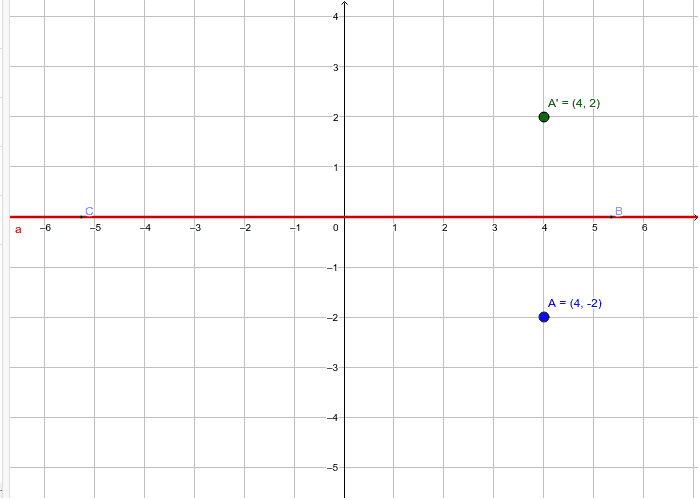



Reflecting Across The X Axis Geogebra




Solved 1 Write The Equation For A F X Reflected In The X Chegg Com
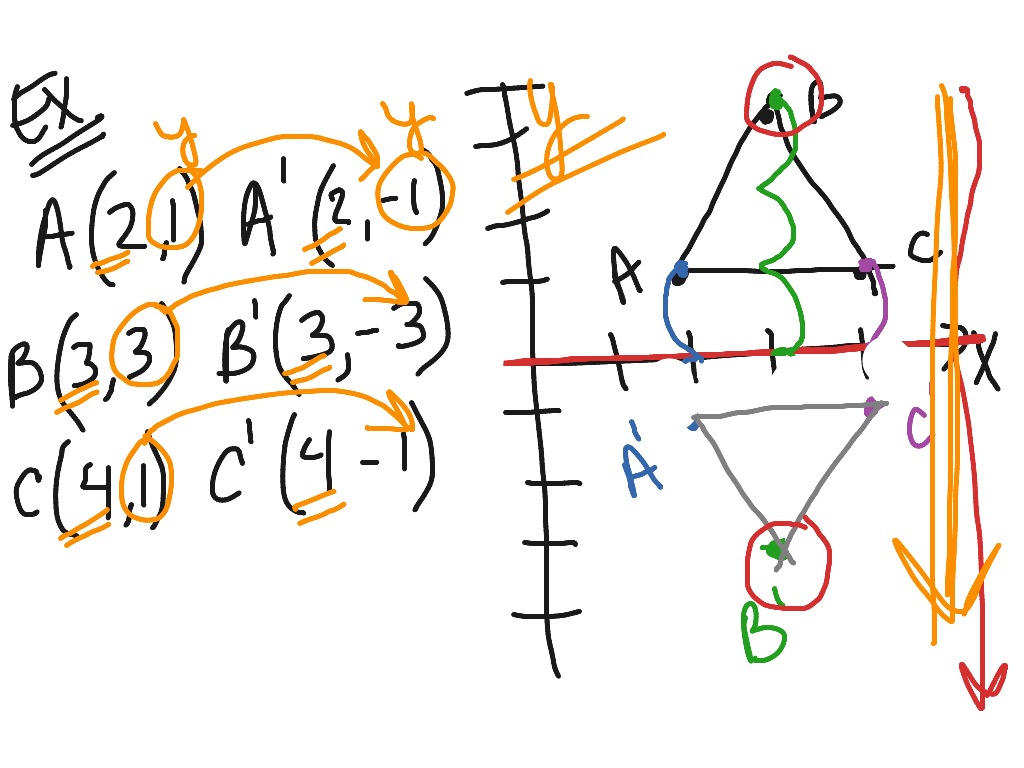



Reflection Over The X Axis Math Showme
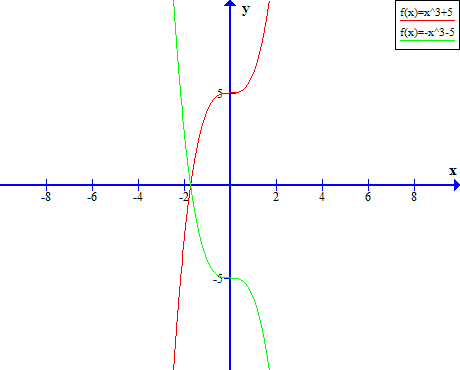



If The Graph Y X 3 5 Is Reflected In The X Axis What Is The New Equation Socratic




Transformation Reflection Over The Line Y X Youtube




Reflections Through The Axes And The Lines Y X And Y X Geogebra
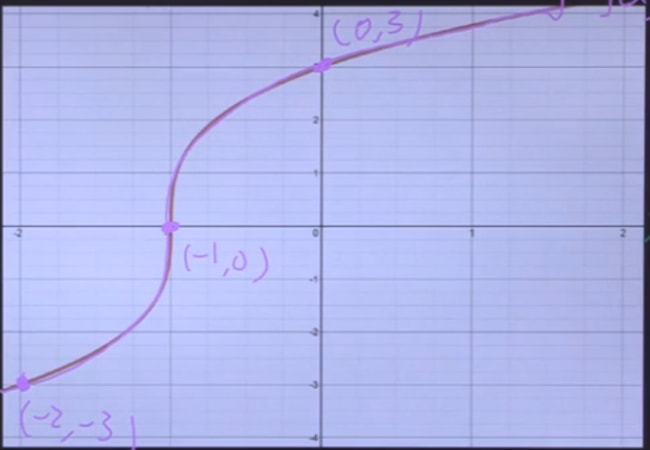



How To Reflect A Graph Through The X Axis Studypug




Ex Reflect A Point About The X Axis Y Axis And The Origin Youtube
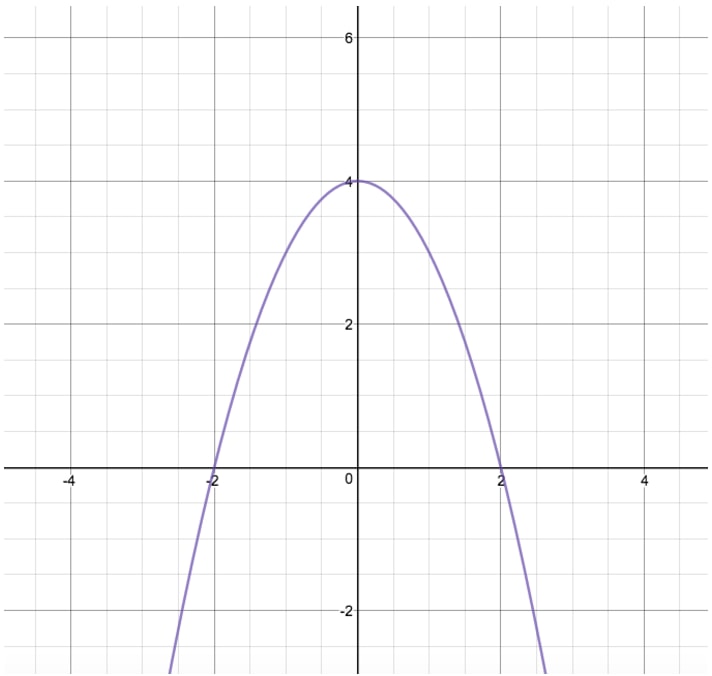



How To Reflect A Graph Through The X Axis Studypug



Y 1 X



Reflections Of A Graph Topics In Precalculus




Reflecting Shapes Article Reflections Khan Academy




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation
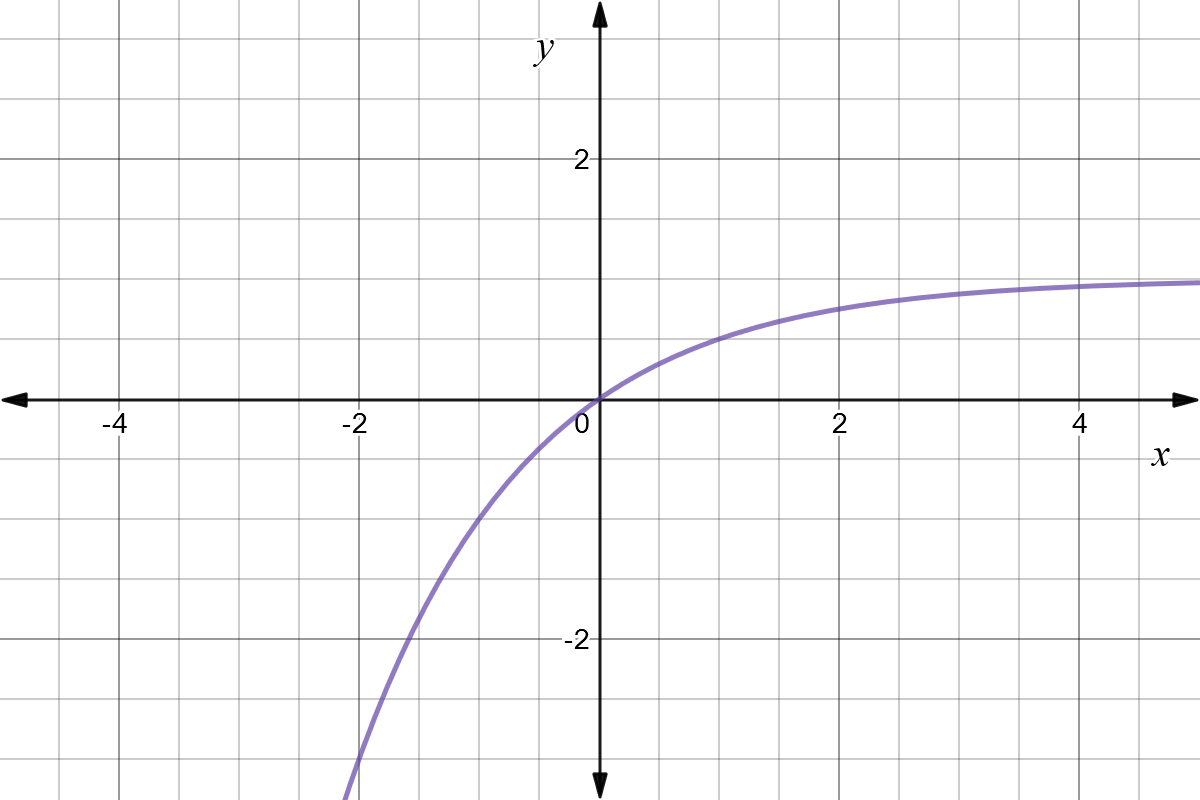



Reflect Function About X Axis F X Expii




Pre Cal 40s Fall 06 Scribe Transformation
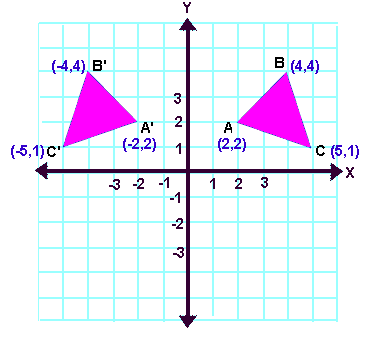



Reflection Transformation
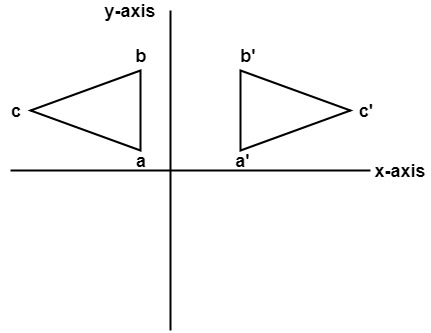



Computer Graphics Reflection Javatpoint



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Please Help Asap I Really Dont Understand Which Transformation Of Y 2 X Will Produce The Graph Brainly Com
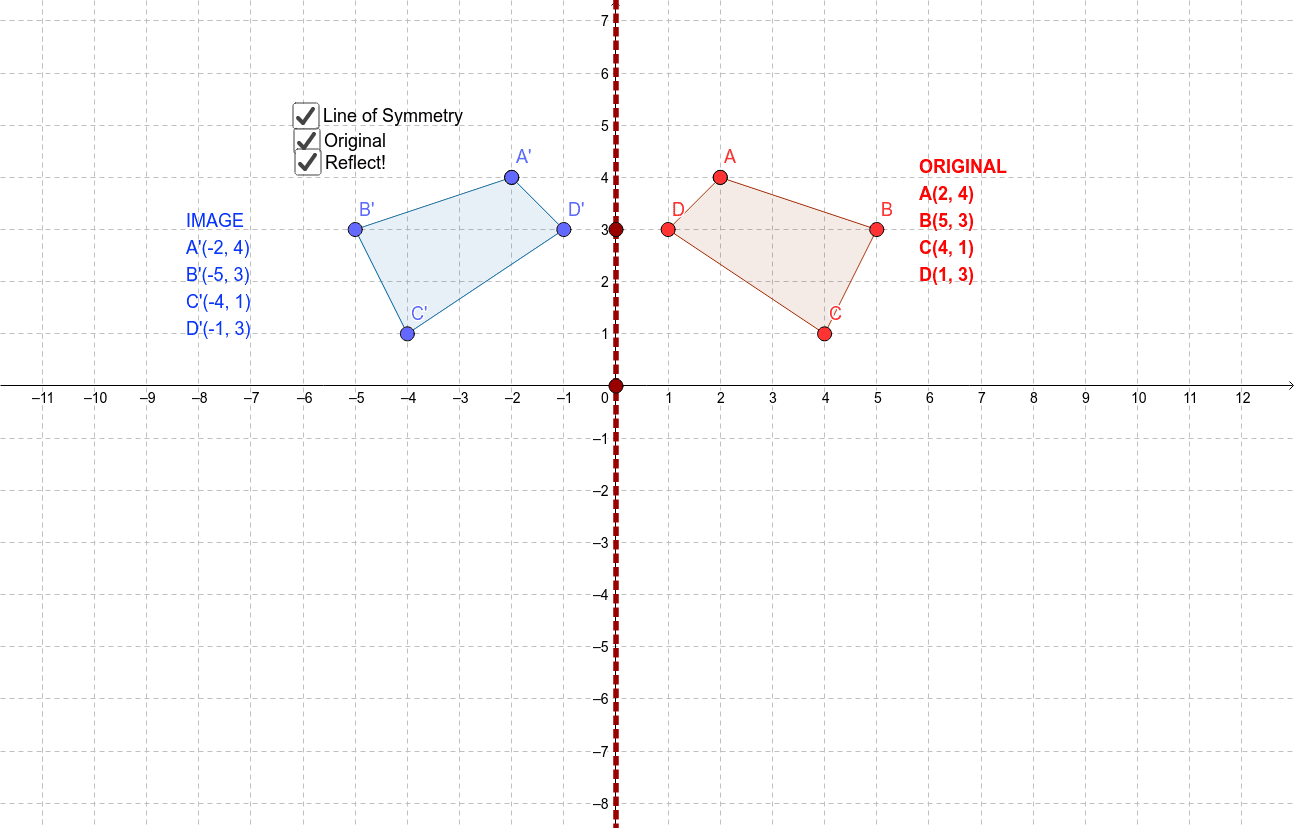



Transformation Reflection Geogebra



Biomath Transformation Of Graphs



Transformations Of Functions
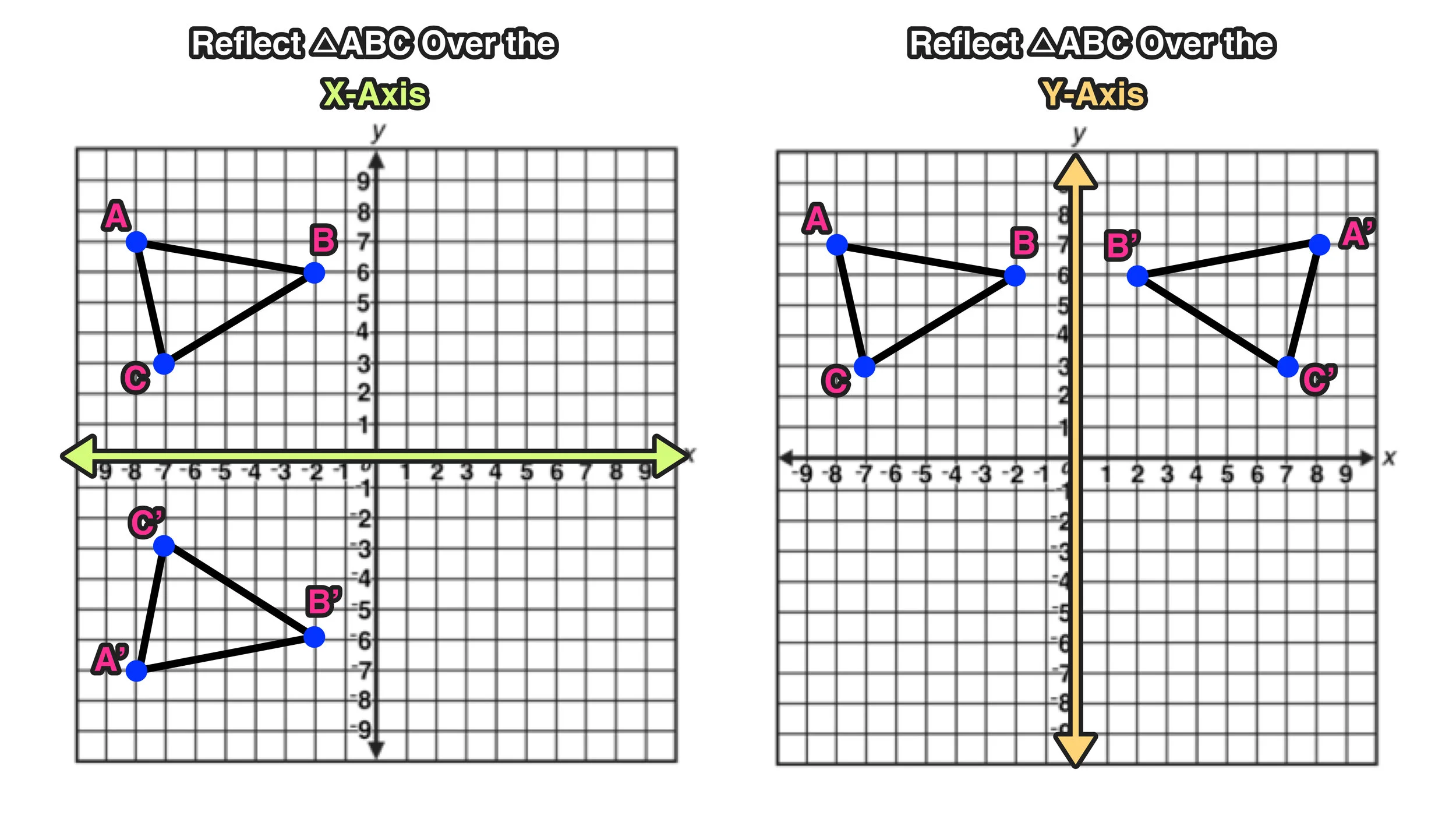



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Reflection Mathbitsnotebook A1 Ccss Math




Want Brainliest Get This Correct Which Rule Should Be Applied To Reflect F X X 3 Over The Brainly Com




Reflect Function About X Axis F X Expii




Reflection Transformation




Reflecting Functions Examples Video Khan Academy
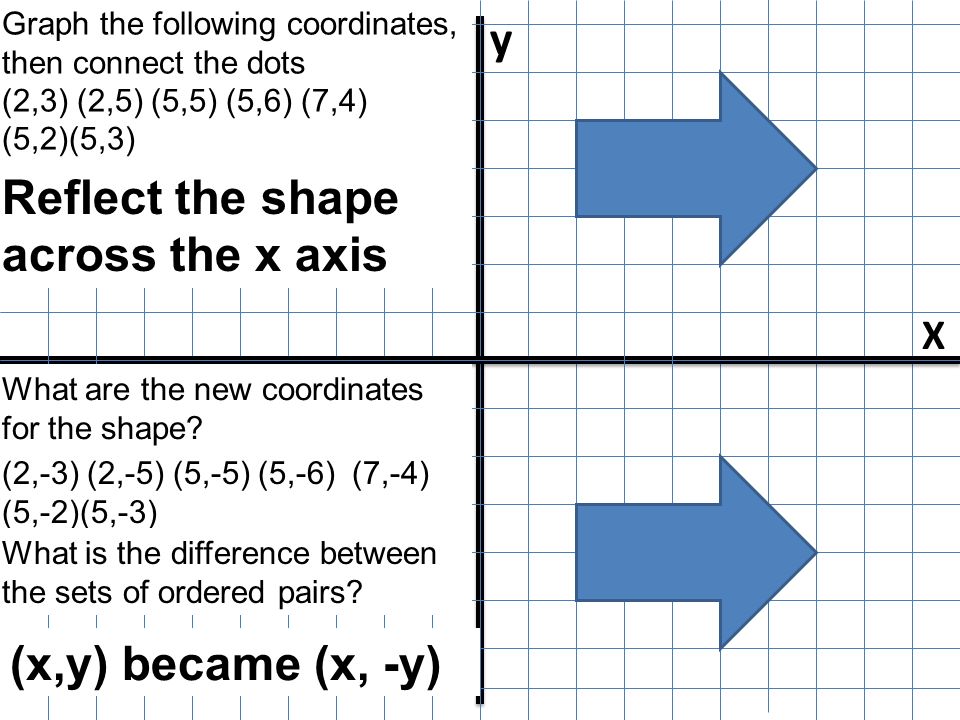



Reflections Reflect The Shape Across The X Axis Graph The Following Coordinates Then Connect The Dots 2 3 2 5 5 5 5 6 7 4 5 2 5 3 What Ppt Download
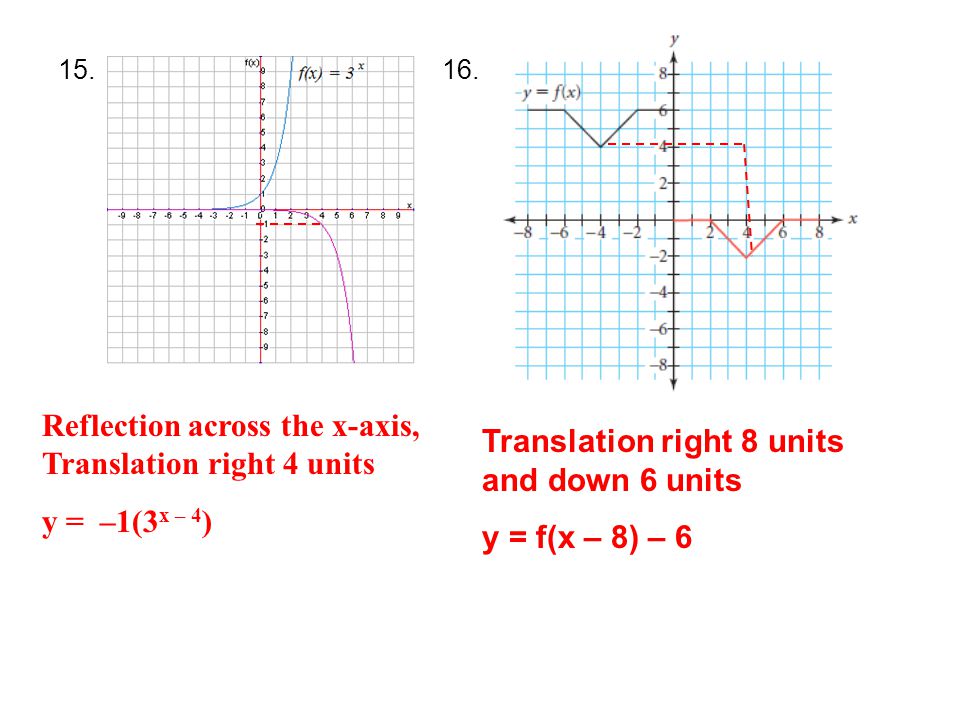



8 3 Notes Handout Ppt Video Online Download




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



Biomath Transformation Of Graphs




Transformations Boundless Algebra
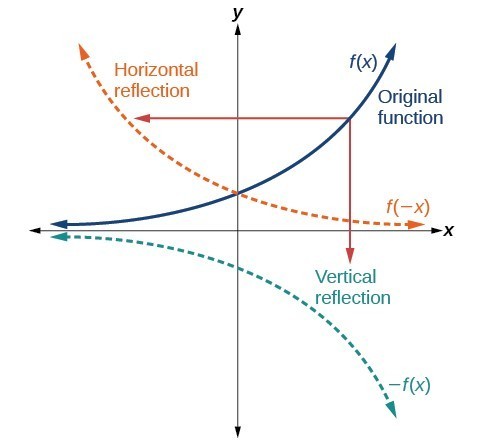



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



Transformations Of Functions Mathbitsnotebook A1 Ccss Math



Reflect Points Across X Axis Y Axis Geogebra
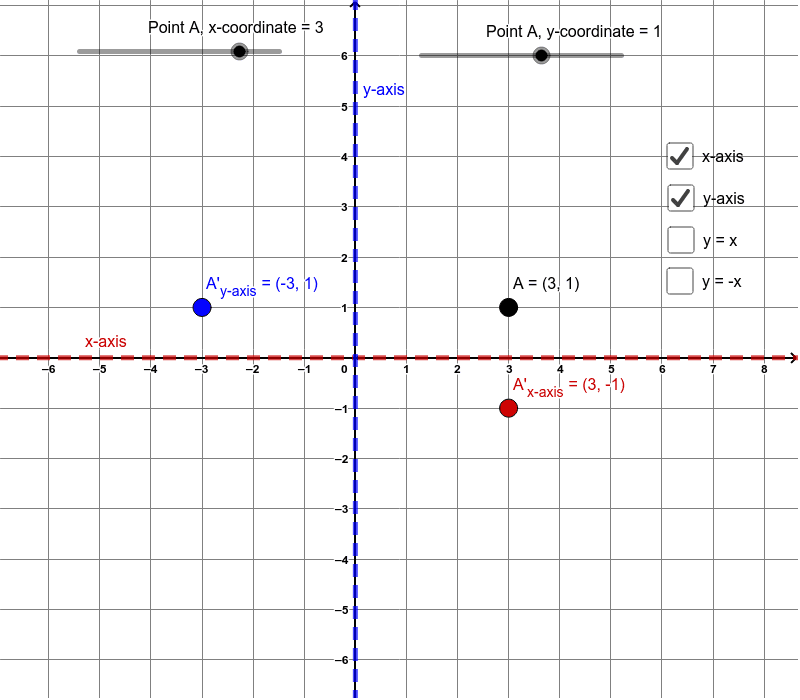



Reflection Rules Geogebra



Solution The Line With The Equation Y 2x 3 Is Reflected In The Y Axis Find The Equation Of The Image Line



What Is The Equation That Represents The Graph Of X 3 X 2 X 1 After It Is Reflected In Both The X Axis And Y Axis Quora



Biomath Transformation Of Graphs




A Line Segment Goes From 1 2 To 4 1 The Line Segment Is Reflected Across X 1 Reflected Across Y 3 And Then Dilated About 2 2 By A Factor




Reflection Mathbitsnotebook A1 Ccss Math




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation




Reflection Across The X Axis Reflection Math Chart




Triangle Jkl Is Translated Using X Y Gt X 1 Y 3 After It Is Reflected Across The Brainly Com



1 5 Shifting Reflecting And Stretching Graphs
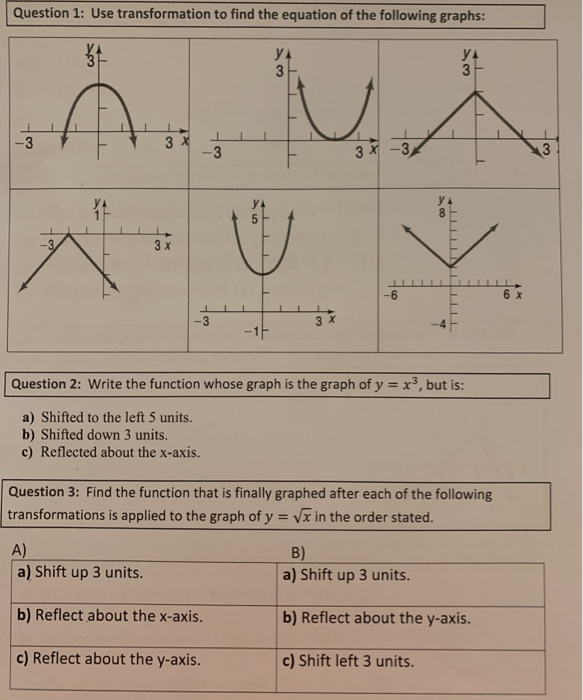



Solved Question 1 Use Transformation To Find The Equation Chegg Com




Reflection Over The X And Y Axis The Complete Guide Mashup Math




Solved The Graph Shown To The Right Involves A Reflection In Chegg Com




What Is The Equation Of This Function After It Is Reflected Over The X Axis Brainly Com
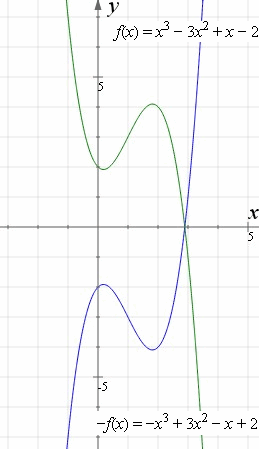



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics
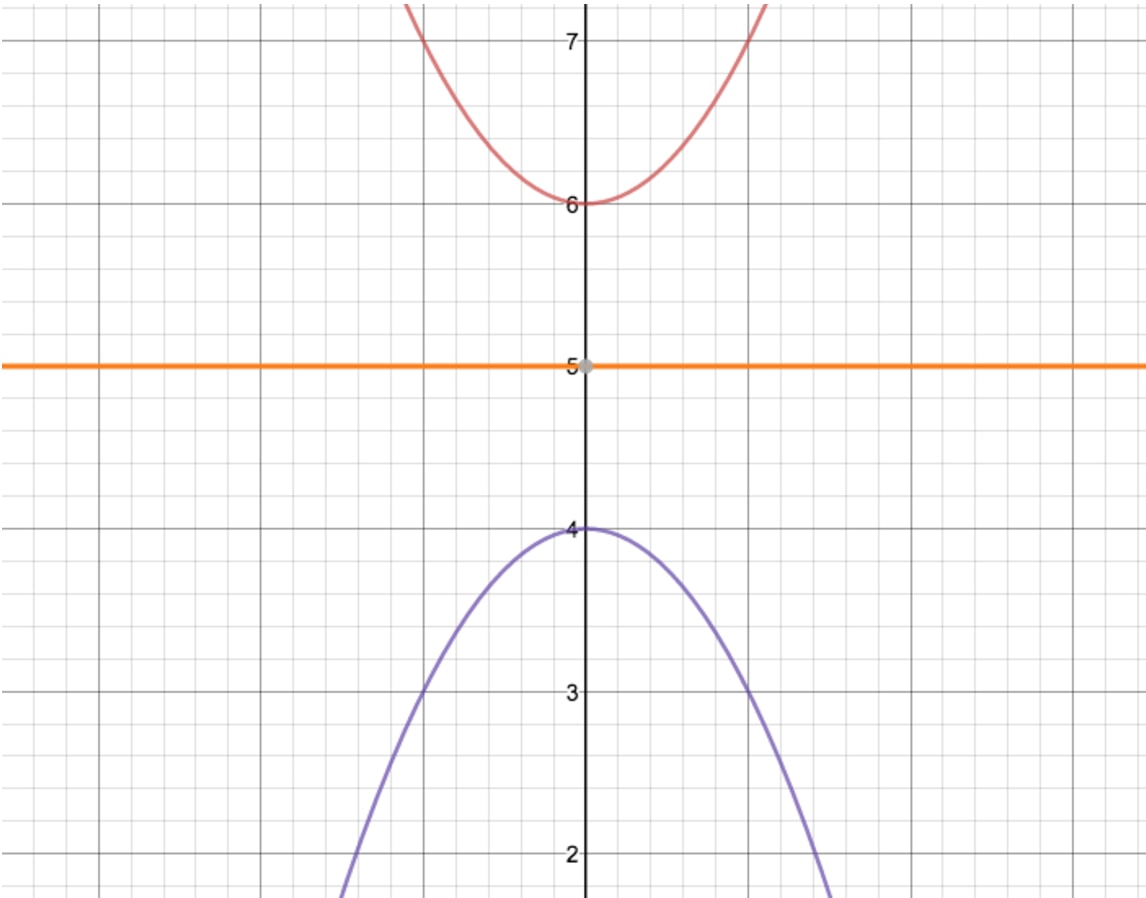



How To Reflect A Graph Through The X Axis Studypug
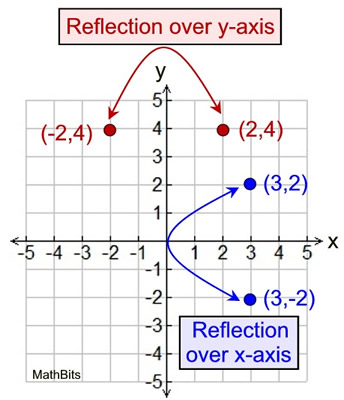



Graphing Coordinate Axes Mathbitsnotebook Jr




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




Solved Question 2 1 Point The Graph Of Y X Is Shift Chegg Com




8 3 Notes Handout Ppt Video Online Download
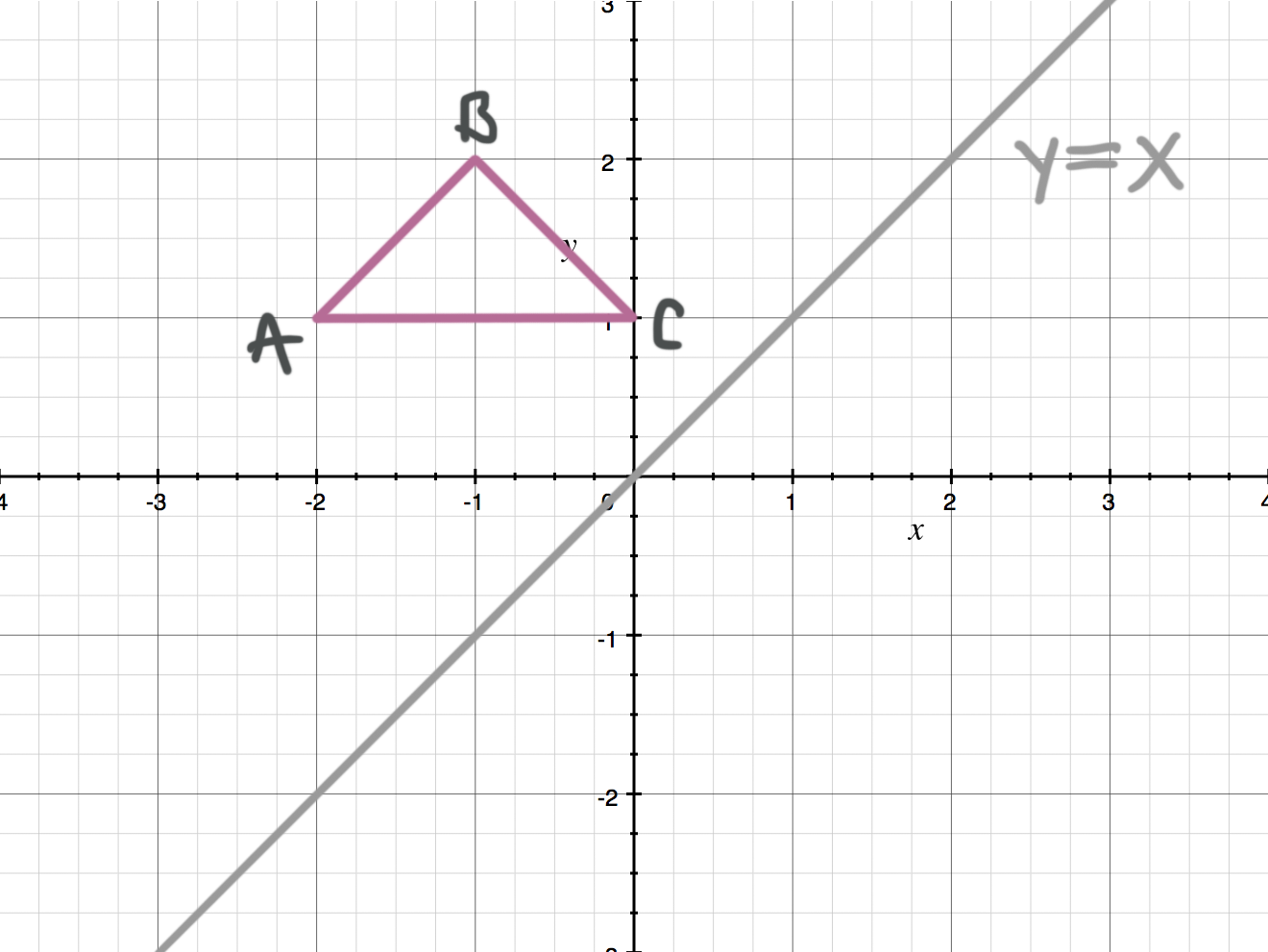



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
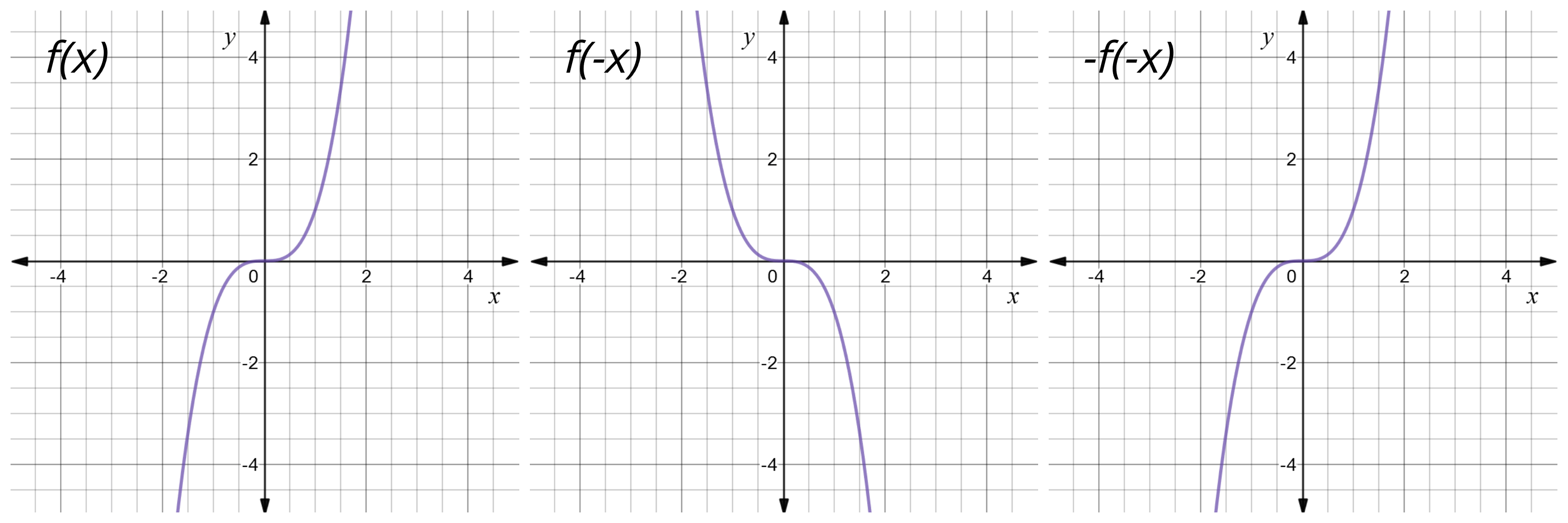



Reflect Function About X Axis F X Expii



Solution What Is The Equation Of The Curve Y X 3 After It Is Reflected In The X Axis




Solved 48 The Graph Of F X 2x Is Reflected Across The Chegg Com



Solution If A 3 5 Is Reflected Over The Y Axis What Are The New Coordinates Of A



Transformation Reflection Over X Axis
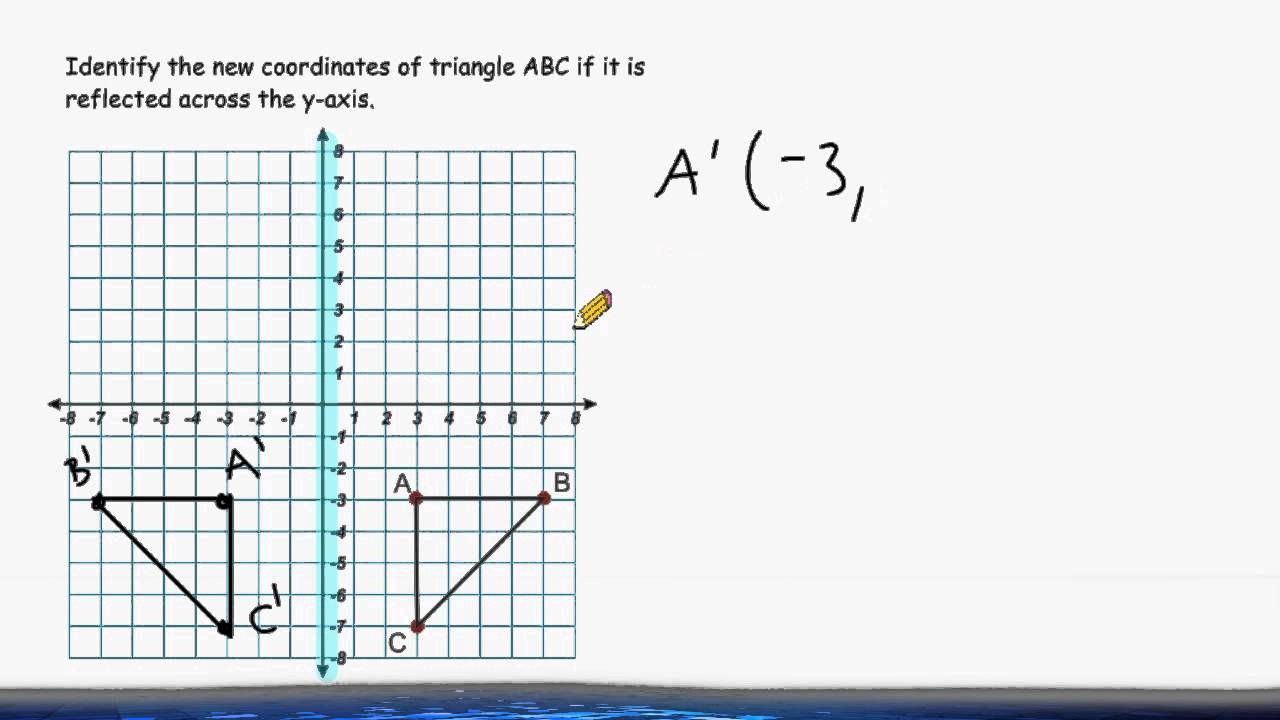



Transformations Reflect A Triangle Across The Y Axis Youtube




Reflection Over The Y X Line Youtube
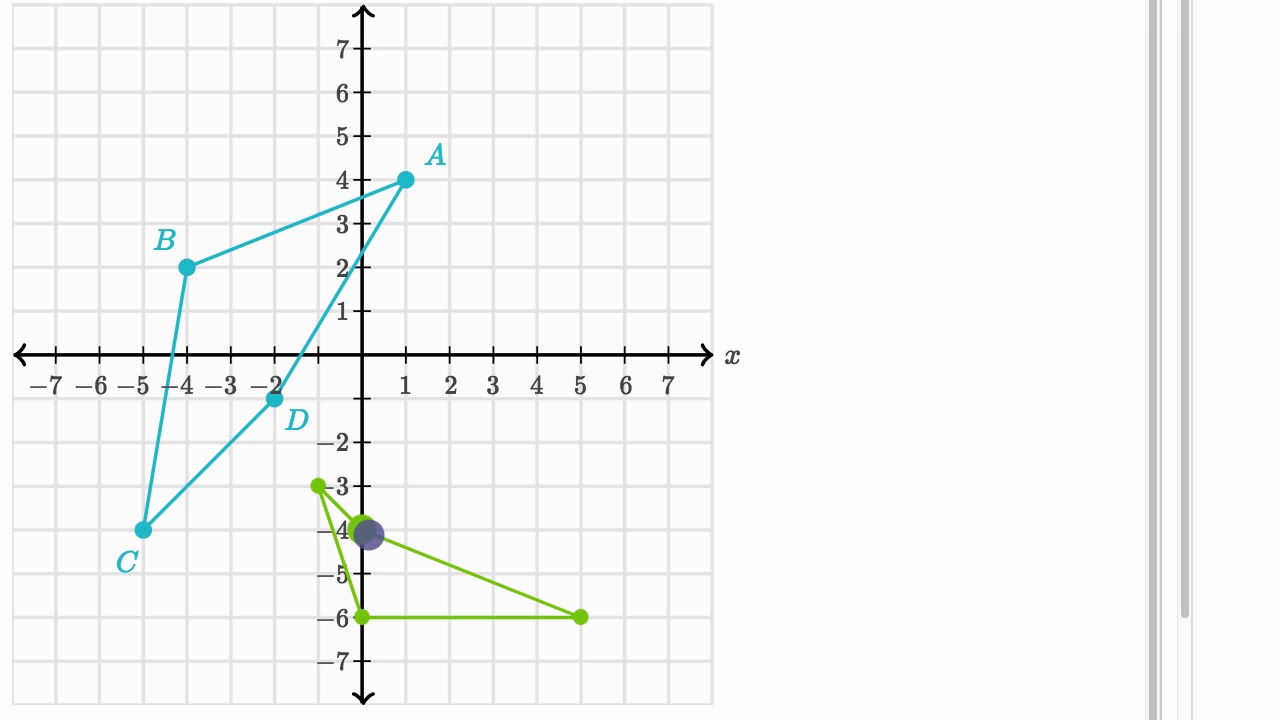



Reflecting Shapes Video Reflections Khan Academy



1
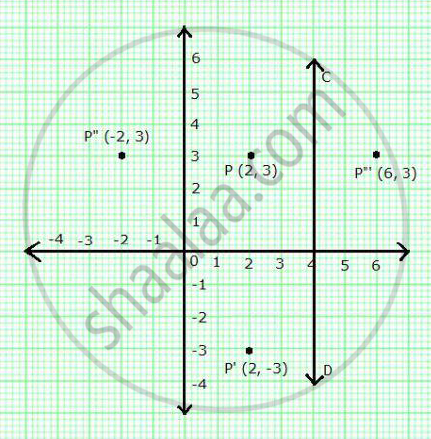



A Point P A B Is Reflected In The X Axis To P 2 3 Write Down The Values Of A And B P Is The Image Of P Reflected In The Y Axis




Reflections Reflect The Shape Across The X Axis Graph The Following Coordinates Then Connect The Dots 2 3 2 5 5 5 5 6 7 4 5 2 5 3 What Ppt Download



Illustrative Mathematics
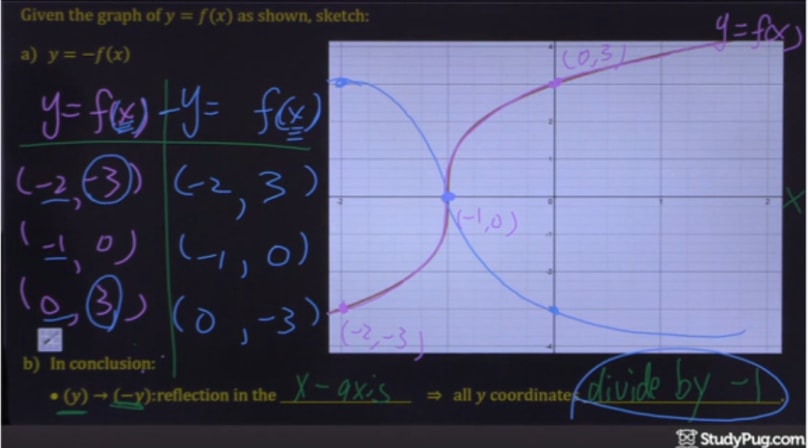



How To Reflect A Graph Through The X Axis Studypug
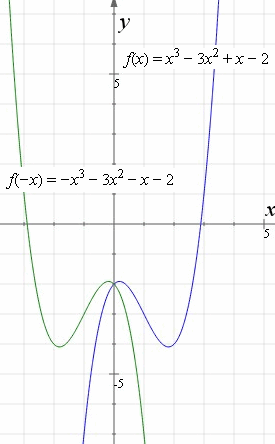



How To Reflect A Graph Through The X Axis Y Axis Or Origin Interactive Mathematics
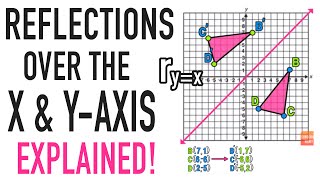



Reflections Over The X Axis And Y Axis Explained Youtube
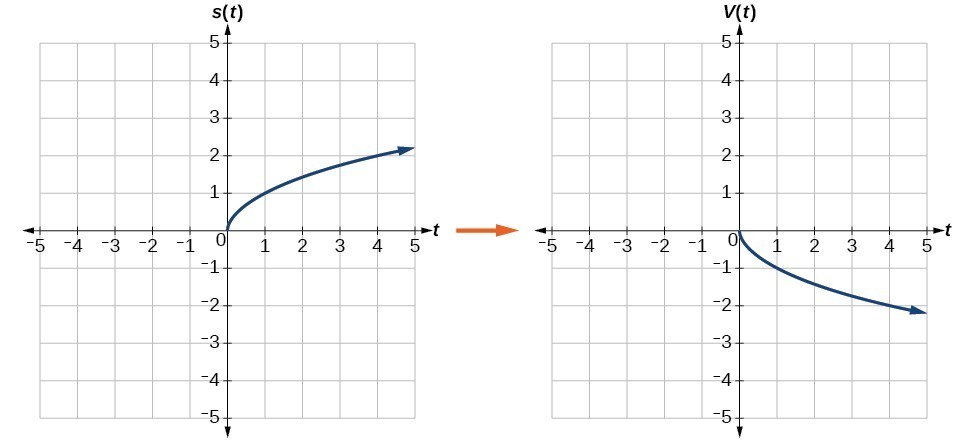



Graph Functions Using Reflections About The X Axis And The Y Axis College Algebra
コメント
コメントを投稿